Это явление объясняется двумя причинами. Во-первых, эклиптика, по которой движется Солнце, наклонена к небесному экватору на угол 23.5 градуса, из-за чего в разные времена года одинаковые приращения эклиптической долготы Солнца дают разные приращения его прямого восхождения. А во-вторых, само Солнце движется по эклиптике неравномерно вследствие неравномерности движения Земли вокруг Солнца (зимой — быстрее, летом — медленнее). В результате совместного влияния этих двух составляющих и получается, что истинные солнечные сутки (промежуток времени между двумя одноименными последовательными кульминациями Солнца) имеют разную продолжительность.
Для устранения непостоянства длительности истинных солнечных суток были введены средние солнечные сутки, равные времени, прошедшему между кульминациями некоторой фиктивной точки, которая движется по небесному экватору со скоростью, равной средней скорости движения истинного Солнца по эклиптике. Соответственно, вместо неравномерного истинного солнечного времени было введено равномерное среднее солнечное время.
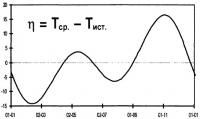
Разность между средним (Тср) и истинным солнечным временем (Тист) и есть уравнение времени (η), кривая которого приведена на графике. Значение уравнения времени плавно меняется на протяжении года в границах от +14m до -16m, четырежды пересекая нулевую отметку. Вычислить уравнение времени довольно просто, если воспользоваться методикой, изложенной Жаном Меесом в его книге "Астрономические формулы для калькуляторов" ("Мир", 1988 г.). Оно вычисляется по формуле:
ЕТ = у sin 2L - 2е sin М + 4е у sin М cos 2L - 0.5у2 sin 4L - 1.25е2 sin 2М
где у = (tg Е/2)2, Е — наклон эклиптики к небесному экватору, L — средняя долгота Солнца, М — средняя аномалия Солнца, е — эксцентриситет орбиты Земли.
В составленной мной программе на заданный день сначала вычисляется юлианская дата (JD); затем время (Т) в юлианских столетиях, прошедшее с 1 января 1900 года; наклон экватора к плоскости эклиптики (ЕК); средняя долгота Солнца (L); средняя аномалия Солнца (М); эксцентриситет орбиты Земли (Е1). Формула для вычисления уравнения времени (Е) разбита на две части и записана в строках 220-225, при этом уравнение времени получается выраженным в радианах. В строке 230 оно преобразуется в минуты. Для перевода радиан в градусы и обратно служит переменная Р1, поскольку перед вычислением уравнения времени все углы переводятся в радианы.
В строках 1000 и 1010 размещена подпрограмма, которая нормализует углы, то есть при обращении к ней в строках 110 и 130 углы (L) и (М) приводятся к диапазону 0-360 градусов.
Во избежание потери точности все переменные в программе имеют двойную точность. Однако, необходимо заметить, что первоначально эта же программа была реализована на "АГАТ", интерпретатор Бейсика которого имел точность 9 знаков после запятой. Этого оказалось вполне достаточно для получения хороших результатов.
В качестве примера определим уравнение времени на 25 июня 1989 года. В результате выполнения программы получим следующие значения переменных:
JD=244702.5
Т=0.894798084
L= 1.625180027
М=2.973280637
ЕК=0.409116512
Е1=0.016713537
Е=2.483306126
Уравнение времени в переменной Е выражено в минутах. Если дробную часть Е преобразовать в секунды, то получим Е=2m29.0s. Табличное значение из переменной части "Астрономического календаря" на 1989 год — 2m27.8s.