В Звездочете №12 за 1999 г. было помещено интересное письмо руководителя Самарского областного центра по реализации программы "Одаренные дети" О. А. Тучина, в котором он обращает внимание на расхождения в указании числа солнечных и лунных затмений в саросе, а также высоты верхней границы хромосферы у авторов учебников и книг по астрономии. Первый вопрос представляет интерес для читателей нашего журнала, потому что дело вовсе не в ошибках авторов книг. Итак, сколько же затмений в саросе)?
Приведем сначала в виде таблички данные, приводимые О. А. Тучиным. Мы указываем только авторов учебников и книг, отсылая за библиографическими данными к письму О. А. Тучина.

Обратимся к наиболее авторитетному источнику в данном вопросе — монографии признанного специалиста по теории затмений А. А. Михайлова "Теория затмений" ("Гостехиздат", 1954 г.). На стр. 23 автор, опираясь на данные "Канона затмений" Т. Оппольцера (1887), пишет: "В течение одного сароса бывает около 43 затмений Солнца и 28 затмений Луны". Обратим внимание на слово "около". Оно означает, что речь идет о многолетнем среднем ("Канон" Оппольцера охватывает промежуток времени в 3369 лет). Именно значения, указанные А. А. Михайловым в своей книге, использовали С. В. Широков и Л. И. Румянцева.
А остальные авторы — что же, ошиблись? Как это ни странно, нет. Все зависит от того, какой интервал времени мы выберем для подсчета среднего числа затмений в саросе. Дело в том, что это число меняется со временем.
Наиболее детальное исследование этого вопроса принадлежит бельгийскому астроному Жану Мейесу, одному из авторов новейшего "Канона затмений" (совместно с германским астрономом Г. Мукке), изданного уже в 1987 г. В своей статье, опубликованной в журнале Ciel et Terre ("Небо и Земля") он приводит любопытные данные, правда, только для лунных затмений. При этом он ссылается еще на один "Канон затмений" — китайского астронома Лю Баолиня, — изданный в 60-е годы.
Оказывается, за двухсотлетие, изученное Лю Баолинем (1964—2163), должно произойти 164 полных затмений Луны, 127 частных и 168 полутене-вых, а всего: теневых 291, а всех — 459. Переводя на длительность сароса (18.03 года), получим число теневых затмений 26, а всех — 41. Но Мейес приводит и изменение этих чисел за пять столетий, начиная с 1601 г. В следующей табличке буквой Т обозначено число полных затмений Луны, буквой Р — число частных. Мы добавили сумму Т+Р, а также пересчет на длину сароса.
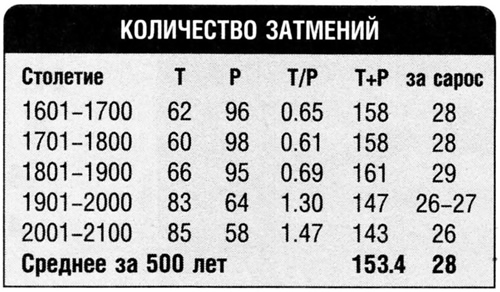
Теперь мы видим, что число лунных затмений в саросе — величина переменная, и глубоко прав был П. В. Щеглов, указавший не среднее число затмений за три с лишним тысячи лет, а крайние возможные значения.
Жан Мейес приводит и число солнечных затмений за ближайшие 200 лет: 452, чему соответствует 41 затмение за сарос. Видимо, это число и использовал В. В. Порфирьев (среднее за последние 200 лет).
Теперь обратим внимание на странное изменение чисел полных и частных затмений Луны на рубеже XIX и XX веков. В это время резко увеличилось число полных затмений Луны за счет частных и общего числа затмений. Видно, с Луной в это время что-то произошло.
Чтобы выяснить, что именно случилось с Луной, вспомним условия наступления лунных затмений. Необходимых условий два: полнолуние и близость Луны к одному из узлов своей орбиты с эклиптикой. Но есть еще одно условие, которое может определить, будет ли затмение полным, частным или полутеневым. Помимо близости ее к узлу многое зависит от того, близка ли Луна в момент затмения к перигею или апогею своей орбиты. Если она близка к перигею, то она глубже войдет в земную тень, и затмение будет полным. Если же к апогею — то оно будет, скорее всего, частным или полутеневым.
Но линия апсид лунной орбиты (перигей-апогей) поворачивается в плоскости орбиты с периодом 8.85 года. Этот период не укладывается целое число раз в саросе (2x8.85=17.7 года). Значит, если в данное затмение Луна была в перигее и затмение было полным, то через сарос она сместится, и затмение будет меньшей фазы, потом еще меньшей и т.д. А грань между полным и частным затмением резкая: если фаза 1.001, то затмение будет полным, а если 0.999, то уже частным. Период этого перехода измеряется столетиями. Вот и вся разгадка.
Осталось разобраться с хромосферой — вторым вопросом, заданным в письме Тучина. Хромосфера Солнца не имеет резко выраженной границы. Она сходит на нет постепенно, по барометрической формуле (как земная атмосфера). Поэтому за условную границу хромосферы принимают уровень, когда плотность достигает определенного значения, или где интенсивность линий излучения составляет, скажем, 1% от максимального значения. Различные ученые используют различные критерии. Так что достаточно сказать, что хромосфера простирается до высоты примерно 10 тыс. км, не стараясь уточнить это значение.



