Проблема 2000: Когда-же начнется третье тысячелетие?

Речь пойдет не о компьютерной проблеме, с ней все ясно: угроза возникла от скупости (в свое время жалко было потратить лишние ячейки дорогостоящей компьютерной памяти для записи даты; кто помнит PC ХТ-286, вздохнет с сочувствием) и разрешилась с большой прибылью для компьютерных фирм. Обсуждаемая здесь "проблема 2000" заключается в том, когда же "на самом деле" начинается новое десятилетие, столетие, тысячелетие.

Кажется, даже тем из "поколения Пепси", кто умеет считать только на пальцах до двадцати, должно быть ясно: второй десяток бутылок начинается с одиннадцатой бутылки. А далее по аналогии: пятая сотня начинается с 401-й бутылки, третья тысяча — с 2001-й. Соответственно, третье тысячелетие должно начинаться с 2001 года. Казалось бы, все ясно. Тем не менее, даже люди с высшим образованием бурно обсуждают эту проблему уже второй год, т.е. год и еще некоторое время, меньшее года (зачем нужно это тривиальное замечание, будет ясно из дальнейшего). Почему же они сомневаются в очевидном, а некоторые даже настаивают на неверном решении? Этот вопрос и составляет для меня Проблему 2000. Попробуем ответить на него.

Люблю ученую аристократию, но с этим ответом не согласен. Невежественный человек ни в чем не сомневается. Если чувствует, что чего-либо не знает, спрашивает у начальства. И еще: неужели половина людей с высшим образованием не знает арифметики в масштабе начальной школы? Нет, первый ответ неверен!

Большинство из нас смотрело по телевизору в последнюю новогоднюю ночь, что происходило в мире. Многомиллиардные прибыли планировал получить связанный с туризмом бизнес (гостиницы, рестораны, воздушный, водный, железнодорожный и автомобильный транспорт, пиротехника, группы артистов всех жанров — всего не перечесть). Неужели эта сила дала бы себя обобрать каким-то "яйцеголовым", что-то бормочущим про неправильный счет?


Возражение: но ведь и при правильном счете фирмы получат те же миллиарды, только на год позже. Да-а, только девственные идеалисты могут сказать такое. Лучше рубль сегодня, чем два рубля через год — таков закон бизнеса. Но главное в другом. Фирмы намеревались удвоить свой доход! Нет никакого сомнения, что если бы прошлогодний "миллениум" принес бы ожидаемую прибыль, уже с нынешней осени, если не с лета, все бы вспомнили о правильном счете. Сослались бы на свою доверчивость к некомпетентным людям и отпраздновали бы начало нового тысячелетия повторно.

Второй ответ правилен. Но не до конца. Червь сомнения попрежнему грызет: должны быть еще и другие причины! Скажем, мы готовимся отпраздновать 300-летие Санкт-Петербурга, основанного в 1703-м году. Ясно, что 300 лет ему стукнет в 2003-м году, и никто не заставит отмечать юбилей на год раньше. (Впрочем, полной уверенности в этом тоже нет. И. В. Сталин отменил 250-летие Ленинграда, а Н. С. Хрущев повелел отпраздновать это событие в 1957-м году, что и было сделано).

Начало отсчета долгот — нулевой меридиан, широт — нулевая параллель (экватор). То же с температурами, высотами над уровнем моря и т.д. и т.п. И в каждом календаре есть начало отсчета, но оно не помечено нулем. Начало юлианского и григорианского календарей помечено первым января 1-го года. Это, действительно, осложняет задачу. Но не сильно. Разве не ясно, что 2000 лет с этого момента пройдут к первому января 2001-го года?

И все же третий ответ правилен. Принятие в качестве начала отсчета цифры 1 сбивает с толку. В школе везде и всюду начало отмечают цифрой 0. Но мне кажется, что перечисленные причины не до конца объясняют явление.

Предыдущие ответы известны специалистам. Последнего я в литературе не встречал. Полагаю, до него додумались и раньше, но не решились опубликовать: вина возлагается на физиков и астрономов, допустивших вопиющую путаницу в счете времени. Поясним ситуацию на примерах.


Представим себе выстроенный в линию ряд (точнее, конечное множество) одинаковых предметов (рис. 1). Условимся считать предметы слева направо. Выделенный на рисунке предмет можно обозначить порядковым числительным "третий". Но можно употребить и количественное числительное "три": столько предметов содержит их подмножество, начинающееся с крайнего левого (этому началу отсчета отвечает цифра 1) и кончающееся выделенным. Таким образом, в дискретном случае допустимо употреблять как количественные, так и порядковые числительные. Недоразумение не возникает.

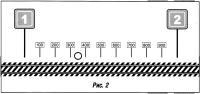
Иная ситуация возникает с непрерывным множеством. Разберем ее сначала на примере измерения расстояний вдоль оси х. Для наглядности ось x: можно отождествить с рельсом на длинном прямолинейном участке (рис. 2). Начало отсчета обозначим цифрой 0 и отметим крупными черточками километры, меньшими — гектометры и т.д. Где находится помеченная кружочком точка? Любой железнодорожник скажет: на 2-м километре. А точнее? На 4-м гектометре 2-го километра. Еще точнее нельзя? На 331-м метре 2-го километра или просто на 1331-м метре. И так далее с повышением точности. Любопытно: четвертый гектометр обернулся трехсотым, а не четырехсотым метром, второй километр — тысячным, а не двухтысячным метром!

Как видим, употребление порядковых числительных неудобно. Наличие нуля как начала отсчета скорее ухудшает ситуацию, чем помогает. Ведь близкие к О точки слева расположены на нулевом километре! Поэтому в науке и технике безраздельно господствует описание измерения непрерывной величины количественными числительными. В нашем примере точка имеет координату х = 1 км 330 м 157 мм = 1.330157 км.


Вот мы и подошли к главному. "Безраздельность" имеет одно исключение: измерение времени. Посмотрим, как описывается засечка времени какого-либо события.

Порядковые числительные

Молния ударила третьего апреля пятнадцатого года на второй секунде третьей минуты в пятом часу. Все как в примере с железнодорожником, только хуже: единицы измерения идут не от крупных к мелким, а в весьма странном с точки зрения логики порядке. Если убрать эту несуразность, то следует поставить в соответствие моменту t порядковое числительное: 15-й год 4-й месяц 3-й день 5-й час 3-я минута 2-я секунда.

Количественные числительные

Очевидно, моменту t соответствует следующее количественное числительное (для простоты мы увеличили точность в сто раз): 14 лет 3 месяца 2 дня 4 часа 2 минуты 1.33 секунды.

Подобная запись исключает даже возможность появления Проблемы 2000. Последний глоток первого бокала шампанского после двенадцатого удара часов в самом начале 2000-го года отвечал бы такой засечке времени: 1999 лет 0 месяцев 0 дней 0 часов 0 минут 33 секунды.

Не повезло времени! Это еще пустяк, что продолжительности более мелких единиц измерения составляют не десятичные доли более крупных, а самые разнообразные, да еще для разных месяцев и лет разные. Главное, что нормальная форма записи с использованием количественных числительных никогда не употребляется.

Смесь порядковых и количественных числительных

В научном отсчете об ударе молнии присутствовало бы примерно такое описание момента t: 15.4.3, 4 часа 2 минуты 1.33 секунд.

Дикая смесь! Первые три числа отвечают порядковым, последние — количественным числительным. Мы к этому привыкли и не замечаем нелепицы. Тем более, что она замаскирована. Ставя дату, мы пишем 03.04.15 вместо 3-го дня 4-го месяца 15-го года.

Ученым все равно, что ставить в соответствие моменту t. На правильность дат исторических событий, а тем более на продолжительность времени между событиями способ записи не влияет. Но если главным укрывателем Ходжи Насреддина был эмир, то главные виновники в Проблеме 2000 — физики и астрономы, использующие химерическую запись моментов времени.


Только ли задача определения начала нового века или тысячелетия усложнена использованием то порядковых, то количественных числительных (в теории множеств Кантора они называются красивыми словами: ординалы и кардиналы)? Нет! Вот примеры.

Пример 1. Чтобы определить ритуальный 50-й день, нужно к дате прибавить число 49.

Пример 2. Чтобы найти число полных дней, проведенных между днем отъезда t₁ и приезда t₂, нужно образовать разность t₂ - t₁. Так оплачивали командировочные 10 лет назад. Число же неполных дней равно t₂ - t₁ + 1. Так оплачивают командировочные сейчас. Уточню, что t₁, t₂ — целые числа, соответствующие дате. Скажем, t₁: 29-е марта, t₂: 2-е апреля (33-е марта), t₂ - t₁ = 4.

Пример 3. Иванов работает через день. Петров работает через два дня на третий. Если обозначить через t₁, t₂ их последовательные рабочие дни, то для Иванова t₂ = t₁ + 2, а для Петрова t₂ = t₁ + 3.

В заключение — вопрос: "Перейдем ли мы когда-либо на нормальную форму записи моментов времени (количественными числительными)?" Думаю, что нет. Астрономы трепетно блюдут традиции. Но все же я не отрицаю такой возможности. На моей памяти за какие-нибудь 50 лет произошел существенный сдвиг в бытовом счислении времени от ординалов к кардиналам. Тогда говорили: четверть десятого. А теперь: 9 часов 15 минут. В определении возраста сдвиг произошел еще раньше. Полтораста лет назад говорили: пошел седьмой год, реже — шестой миновал. А теперь: исполнилось шесть лет. К радости прекрасного пола. Все же приятнее, когда тебе 39 лет, а не сороковой год. Еще приятнее, когда тебе 41 год, а не пятый десяток лет.